гҖҖгҖҖжғіиҰҒеҸӮеҠ 2022е№ҙеҶӣйҳҹж–ҮиҒҢиҖғиҜ•зҡ„иҖғз”ҹпјҢзҺ°еңЁе°ұеҸҜд»ҘзқҖжүӢеӨҮиҖғдәҶпјҢдёәдәҶеё®еҠ©еӨҮиҖғйғЁйҳҹж–ҮиҒҢиҖғиҜ•еҗҢеӯҰдәҶи§Је…ЁеҶӣйқўеҗ‘зӨҫдјҡе…¬ејҖжӢӣиҖғж–ҮиҒҢдәәе‘ҳз»ҹдёҖиҖғиҜ•е…¬е…ұ科зӣ®зҡ„жөӢжҹҘиҢғеӣҙгҖҒиҖғд»Җд№ҲеҶ…е®№е’ҢиҰҒжұӮпјҢд»ҘеҸҠзңҹйўҳйўҳеһӢиҝӣиЎҢи§Јзӯ”гҖӮ
гҖҖгҖҖеҶӣйҳҹж–ҮиҒҢе…¬е…ұ科зӣ®еҢ…жӢ¬е…¬е…ұеҹәзЎҖе’ҢеІ—дҪҚиғҪеҠӣпјҢеІ—дҪҚиғҪеҠӣжңүиҜӯйҹізҗҶи§ЈдёҺиЎЁиҫҫгҖҒж•°йҮҸе…ізі»гҖҒеҲӨж–ӯжҺЁзҗҶгҖҒиө„ж–ҷеҲҶжһҗ科зӣ®гҖӮ
гҖҖгҖҖ1.дё–з•ҢжқҜжңү32ж”Ҝи¶ізҗғйҳҹеҸӮеҠ жҜ”иөӣгҖӮ32ж”Ҝзҗғйҳҹиў«еҲҶжҲҗ8дёӘе°Ҹз»„пјҢжҜҸдёӘе°Ҹз»„4ж”ҜзҗғйҳҹгҖӮе…ҲиҝӣиЎҢе°Ҹз»„иөӣгҖӮеңЁе°Ҹз»„иөӣйҳ¶ж®өпјҢеҗ„дёӘе°Ҹз»„зҡ„4ж”ҜзҗғйҳҹиҝӣиЎҢеҚ•еҫӘзҺҜжҜ”иөӣгҖӮе°Ҹз»„иөӣйҳ¶ж®өжҜ”иөӣзҡ„еңәж¬ЎжҳҜ( )еңәгҖӮ
гҖҖгҖҖA.24
гҖҖгҖҖB.36
гҖҖгҖҖC.48
гҖҖгҖҖD.31
гҖҖгҖҖгҖҗзӯ”жЎҲгҖ‘C
гҖҖгҖҖгҖҗи§ЈжһҗгҖ‘
гҖҖгҖҖ第дёҖжӯҘпјҢжң¬йўҳиҖғжҹҘжҜ”иөӣй—®йўҳпјҢз”ЁеҚ•еҫӘзҺҜиөӣе…¬ејҸи§ЈйўҳгҖӮ
гҖҖгҖҖ第дәҢжӯҘпјҢз”ұжҜҸдёӘе°Ҹз»„4ж”ҜзҗғйҳҹиҝӣиЎҢеҚ•еҫӘзҺҜжҜ”иөӣпјҢеҸҜеҫ—жҜҸдёӘе°Ҹз»„еҶ…йғЁзҡ„жҜ”иөӣеңәж¬Ўж•°дёә(еңә)гҖӮ
гҖҖгҖҖ第дёүжӯҘпјҢ32ж”ҜзҗғйҳҹеҲҶжҲҗ8дёӘе°Ҹз»„пјҢжҜҸдёӘе°Ҹз»„йңҖиҰҒиҝӣиЎҢ6еңәжҜ”иөӣпјҢйӮЈд№Ҳж•ҙдёӘе°Ҹз»„иөӣйҳ¶ж®өжҜ”иөӣеңәж¬Ўж•°е…ұжңү8×6=48(еңә)гҖӮ
гҖҖгҖҖеӣ жӯӨпјҢйҖүжӢ©CйҖүйЎ№гҖӮ
гҖҖгҖҖгҖҗжӢ“еұ•гҖ‘
гҖҖгҖҖгҖҗж ҮзӯҫгҖ‘
гҖҖгҖҖгҖҗзҹҘиҜҶзӮ№гҖ‘жҜ”иөӣй—®йўҳ
гҖҖгҖҖгҖҗйҡҫеәҰгҖ‘дёӯзӯү
гҖҖгҖҖ2.жҡ‘еҒҮйҮҢд№җд№җжҠҘеҗҚеҸӮеҠ дәҶжёёжіігҖҒз»ҳз”»е’Ңи·ҶжӢійҒ“зӯүдёүдёӘе…ҙи¶ЈзҸӯпјҢе…¶дёӯжёёжіізҸӯжҜҸйҡ”2еӨ©дёҠдёҖж¬ЎиҜҫпјҢз»ҳз”»зҸӯжҜҸйҡ”3еӨ©дёҠдёҖж¬ЎиҜҫпјҢи·ҶжӢійҒ“жҜҸйҡ”6еӨ©дёҠдёҖж¬ЎиҜҫгҖӮе·ІзҹҘ7жңҲ1ж—Ҙд№җд№җеңЁиҝҷдёүдёӘе…ҙи¶ЈзҸӯйғҪдёҠдәҶиҜҫпјҢеҲҷд»–еңЁ7гҖҒ8дёӨдёӘжңҲдёӯдёҚз”ЁдёҠиҝҷдёүдёӘе…ҙи¶ЈзҸӯзҡ„еӨ©ж•°жҳҜ( )еӨ©гҖӮ
гҖҖгҖҖA.25
гҖҖгҖҖB.26
гҖҖгҖҖC.28
гҖҖгҖҖD.27
гҖҖгҖҖгҖҗзӯ”жЎҲгҖ‘D
гҖҖгҖҖгҖҗи§ЈжһҗгҖ‘
гҖҖгҖҖи§Јжі•дёҖпјҡ
гҖҖгҖҖ第дёҖжӯҘпјҢжң¬йўҳиҖғжҹҘжҳҹжңҹж—Ҙжңҹй—®йўҳпјҢз”Ёжһҡдёҫжі•и§ЈйўҳгҖӮ
гҖҖгҖҖ第дёҖжӯҘпјҢ7жңҲ1ж—ҘдёүдёӘе…ҙи¶ЈзҸӯйғҪдёҠдәҶиҜҫпјҢеҲҷ7—8жңҲдёӯпјҢдёҠиҜҫжғ…еҶөеҰӮдёӢиЎЁпјҡ
гҖҖгҖҖ(дёҠжёёжііиҜҫз”Ё√пјҢдёҠз»ҳз”»иҜҫз”Ёв—ӢпјҢдёҠи·ҶжӢійҒ“иҜҫз”Ёв–іпјҢж— иҜҫз”Ё×)
гҖҖгҖҖе…ұжңү27еӨ©дёҚз”ЁдёҠиҝҷдёүдёӘе…ҙи¶ЈзҸӯгҖӮ
гҖҖгҖҖеӣ жӯӨпјҢйҖүжӢ©DйҖүйЎ№гҖӮ
гҖҖгҖҖи§Јжі•дәҢпјҡ
гҖҖгҖҖ第дёҖжӯҘпјҢжң¬йўҳиҖғжҹҘжҳҹжңҹж—Ҙжңҹй—®йўҳпјҢз”Ёе®№ж–ҘеҺҹзҗҶзӣёе…ізҹҘиҜҶи§ЈйўҳгҖӮ
гҖҖгҖҖ第дәҢжӯҘпјҢ7жңҲе’Ң8жңҲйғҪжҳҜеӨ§жңҲпјҢеҗ„жңү31еӨ©пјҢе…ұ62еӨ©пјҢ7жңҲ1ж—ҘдёүдёӘиҜҫйғҪдёҠпјҢеҸӘи®Ёи®әеү©дёӢзҡ„61еӨ©пјҢжёёжіізҸӯдёҠиҜҫ61÷3=20……1пјҢеҚідёҠиҜҫ20еӨ©;з»ҳз”»зҸӯдёҠиҜҫ61÷4=15……1пјҢеҚідёҠиҜҫ15еӨ©;и·ҶжӢійҒ“зҸӯдёҠиҜҫ61÷7=8……5пјҢеҚідёҠиҜҫ8еӨ©гҖӮеҗҢж—¶дёҠжёёжііе’Ңз»ҳз”»зҸӯзҡ„жңү61÷12(3е’Ң4зҡ„жңҖе°Ҹе…¬еҖҚж•°)=5……1пјҢеҚі5еӨ©;еҗҢж—¶дёҠжёёжііе’Ңи·ҶжӢійҒ“зҸӯзҡ„жңү61÷21=2……19;еҗҢж—¶дёҠз»ҳз”»е’Ңи·ҶжӢійҒ“зҸӯзҡ„жңү61÷28=2……5пјҢеҚі2еӨ©пјҢдёүдёӘиҜҫйғҪдёҠзҡ„жІЎжңүпјҢеӣ жӯӨе…ұдёҠиҜҫ20+15+8-5-2-2=34(еӨ©)пјҢйӮЈд№Ҳжңү61-34=27(еӨ©)дёүдёӘиҜҫйғҪдёҚз”ЁдёҠгҖӮ
гҖҖгҖҖеӣ жӯӨпјҢйҖүжӢ©DйҖүйЎ№гҖӮ
гҖҖгҖҖгҖҗжӢ“еұ•гҖ‘
гҖҖгҖҖгҖҗж ҮзӯҫгҖ‘
гҖҖгҖҖгҖҗзҹҘиҜҶзӮ№гҖ‘жҳҹжңҹж—Ҙжңҹй—®йўҳ
гҖҖгҖҖгҖҗйҡҫеәҰгҖ‘дёӯзӯү
гҖҖгҖҖ3.1896пјҢ1948пјҢ1988пјҢ2000пјҢ2012пјҢ2020пјҢдёӢеҲ—е№ҙеәҰдёӯдёҺдёҠиҝ°е№ҙеәҰе…·жңүзӣёеҗҢзҡ„规еҫӢзҡ„е№ҙеәҰжҳҜ( )е№ҙгҖӮ
гҖҖгҖҖA.1600
гҖҖгҖҖB.1900
гҖҖгҖҖC.2010
гҖҖгҖҖD.2018
гҖҖгҖҖгҖҗзӯ”жЎҲгҖ‘A
гҖҖгҖҖгҖҗи§ЈжһҗгҖ‘
гҖҖгҖҖ第дёҖжӯҘпјҢжң¬йўҳиҖғжҹҘжҳҹжңҹж—Ҙжңҹй—®йўҳгҖӮ
гҖҖгҖҖ第дәҢжӯҘпјҢж №жҚ®й—°е№ҙеҲӨе®ҡжі•еҲҷпјҡйқһж•ҙзҷҫе№ҙе№ҙд»ҪиғҪиў«4ж•ҙйҷӨжҲ–ж•ҙзҷҫе№ҙд»ҪиғҪиў«400ж•ҙйҷӨзҡ„дёәй—°е№ҙгҖӮйўҳе№Ідёӯз»ҷеҮәзҡ„1896пјҢ1948пјҢ1988пјҢ2000пјҢ2012пјҢ2020йғҪжҳҜй—°е№ҙпјҢи§ӮеҜҹйҖүйЎ№еҸ‘зҺ°пјҢеҸӘжңү1600е№ҙжҳҜй—°е№ҙгҖӮ
гҖҖгҖҖеӣ жӯӨпјҢйҖүжӢ©AйҖүйЎ№гҖӮ
гҖҖгҖҖгҖҗжӢ“еұ•гҖ‘
гҖҖгҖҖгҖҗж ҮзӯҫгҖ‘
гҖҖгҖҖгҖҗзҹҘиҜҶзӮ№гҖ‘жҳҹжңҹж—Ҙжңҹй—®йўҳ
гҖҖгҖҖгҖҗйҡҫеәҰгҖ‘дёӯзӯү
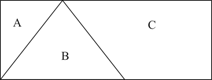
гҖҖгҖҖ4.е°ҶдёҖеқ—й•ҝ10еҺҳзұігҖҒе®Ҫ4еҺҳзұізҡ„й•ҝж–№еҪўе№іжқҝеҲҮеүІжҲҗAгҖҒBгҖҒCе…ұ3еқ—пјҢе…¶дёӯCеқ—зҡ„йқўз§Ҝдёә22е№іж–№еҺҳзұіпјҢBдёәзӯүи…°дёүи§’еҪўпјҢйӮЈд№ҲAеқ—зҡ„йқўз§ҜжҳҜ( )гҖӮ
 гҖҖгҖҖA.6е№іж–№еҺҳзұі
гҖҖгҖҖA.6е№іж–№еҺҳзұі
гҖҖгҖҖB.12е№іж–№еҺҳзұі
гҖҖгҖҖC.8е№іж–№еҺҳзұі
гҖҖгҖҖD.4е№іж–№еҺҳзұі
гҖҖгҖҖгҖҗзӯ”жЎҲгҖ‘A
гҖҖгҖҖгҖҗи§ЈжһҗгҖ‘
гҖҖгҖҖ第дёҖжӯҘпјҢжң¬йўҳиҖғжҹҘеҮ дҪ•й—®йўҳпјҢеұһдәҺе№ійқўеҮ дҪ•зҡ„йқўз§Ҝи®Ўз®—й—®йўҳгҖӮ
гҖҖгҖҖ第дәҢжӯҘпјҢй•ҝж–№еҪўзҡ„й•ҝдёә10еҺҳзұіпјҢе®Ҫдёә4еҺҳзұіпјҢйӮЈд№ҲиҜҘзҹ©еҪўзҡ„йқўз§Ҝдёә10×4=40(е№іж–№еҺҳзұі)пјҢCзҡ„йқўз§Ҝдёә22е№іж–№еҺҳзұіпјҢйӮЈд№ҲA+Bзҡ„йқўз§Ҝдёә40-22=18(е№іж–№еҺҳзұі)гҖӮеҒҡдёүи§’еҪўBзҡ„еһӮзәҝпјҢеҰӮеӣҫжүҖзӨәпјҢBдёәзӯүи…°дёүи§’еҪўпјҢеҲҷдёүзәҝеҗҲдёҖпјҢйӮЈд№ҲеҸҜеҫ—дёүи§’еҪўAзҡ„йқўз§Ҝдёәдёүи§’еҪўBзҡ„йқўз§Ҝзҡ„дёҖеҚҠпјҢеҲҷв–іBзҡ„йқўз§Ҝ=2×в–іAзҡ„йқўз§ҜгҖӮйӮЈд№Ҳв–іAзҡ„йқўз§Ҝдёә18/3=6(е№іж–№еҺҳзұі)гҖӮ
гҖҖгҖҖеӣ жӯӨпјҢйҖүжӢ©AйҖүйЎ№гҖӮ
гҖҖгҖҖгҖҗжӢ“еұ•гҖ‘
гҖҖгҖҖгҖҗж ҮзӯҫгҖ‘
гҖҖгҖҖгҖҗзҹҘиҜҶзӮ№гҖ‘е№ійқўеҮ дҪ•зұ»
гҖҖгҖҖгҖҗйҡҫеәҰгҖ‘дёӯзӯү
гҖҖгҖҖ5.е·ҘеҺӮз”ҹдә§дёҖжү№дә§е“ҒпјҢ18еҗҚе·ҘдәәйңҖ3.5е°Ҹж—¶жүҚиғҪе®ҢжҲҗгҖӮзҺ°йңҖжҸҗеүҚ0.5е°Ҹж—¶е®ҢжҲҗпјҢеҒҮи®ҫе·Ҙдәәе·ҘдҪңж•ҲзҺҮзӣёеҗҢпјҢеҲҷйңҖеўһеҠ е·Ҙдәәзҡ„дәәж•°жҳҜ( )дәәгҖӮ
гҖҖгҖҖA.1
гҖҖгҖҖB.2
гҖҖгҖҖC.3
гҖҖгҖҖD.4
гҖҖгҖҖгҖҗзӯ”жЎҲгҖ‘C
гҖҖгҖҖгҖҗи§ЈжһҗгҖ‘
гҖҖгҖҖ第дёҖжӯҘпјҢжң¬йўҳиҖғжҹҘе·ҘзЁӢй—®йўҳпјҢз”ЁиөӢеҖјжі•и§ЈйўҳгҖӮ
гҖҖгҖҖ第дәҢжӯҘпјҢиөӢеҖјжҜҸеҗҚе·Ҙдәәзҡ„ж•ҲзҺҮдёә1пјҢйӮЈд№Ҳ18еҗҚе·Ҙдәәзҡ„ж•ҲзҺҮдёә18пјҢйңҖиҰҒ3.5е°Ҹж—¶жүҚиғҪе®ҢжҲҗпјҢиҜҙжҳҺиҝҷжү№дә§е“Ғзҡ„жҖ»йҮҸдёә18×3.5=63пјҢиҰҒжғіжҸҗеүҚ0.5е°Ҹж—¶е®ҢжҲҗпјҢеҲҷз”Ёж—¶3.5-0.5=3(е°Ҹж—¶)пјҢйӮЈд№Ҳж•ҲзҺҮйңҖиҰҒиҫҫеҲ°63/3=21пјҢеҚійңҖиҰҒ21еҗҚе·ҘдәәпјҢйңҖиҰҒеўһеҠ 21-18=3(дәә)гҖӮ
гҖҖгҖҖеӣ жӯӨпјҢйҖүжӢ©CйҖүйЎ№гҖӮ
гҖҖгҖҖгҖҗжӢ“еұ•гҖ‘
гҖҖгҖҖгҖҗж ҮзӯҫгҖ‘
гҖҖгҖҖгҖҗзҹҘиҜҶзӮ№гҖ‘ж•ҲзҺҮзұ»
гҖҖгҖҖгҖҗйҡҫеәҰгҖ‘дёӯзӯү
гҖҖгҖҖеҶӣйҳҹж–ҮиҒҢе…¬е…ұ科зӣ®еҢ…жӢ¬е…¬е…ұеҹәзЎҖе’ҢеІ—дҪҚиғҪеҠӣпјҢеІ—дҪҚиғҪеҠӣжңүиҜӯйҹізҗҶи§ЈдёҺиЎЁиҫҫгҖҒж•°йҮҸе…ізі»гҖҒеҲӨж–ӯжҺЁзҗҶгҖҒиө„ж–ҷеҲҶжһҗ科зӣ®гҖӮ
гҖҖгҖҖ1.дё–з•ҢжқҜжңү32ж”Ҝи¶ізҗғйҳҹеҸӮеҠ жҜ”иөӣгҖӮ32ж”Ҝзҗғйҳҹиў«еҲҶжҲҗ8дёӘе°Ҹз»„пјҢжҜҸдёӘе°Ҹз»„4ж”ҜзҗғйҳҹгҖӮе…ҲиҝӣиЎҢе°Ҹз»„иөӣгҖӮеңЁе°Ҹз»„иөӣйҳ¶ж®өпјҢеҗ„дёӘе°Ҹз»„зҡ„4ж”ҜзҗғйҳҹиҝӣиЎҢеҚ•еҫӘзҺҜжҜ”иөӣгҖӮе°Ҹз»„иөӣйҳ¶ж®өжҜ”иөӣзҡ„еңәж¬ЎжҳҜ( )еңәгҖӮ
гҖҖгҖҖA.24
гҖҖгҖҖB.36
гҖҖгҖҖC.48
гҖҖгҖҖD.31
гҖҖгҖҖгҖҗзӯ”жЎҲгҖ‘C
гҖҖгҖҖгҖҗи§ЈжһҗгҖ‘
гҖҖгҖҖ第дёҖжӯҘпјҢжң¬йўҳиҖғжҹҘжҜ”иөӣй—®йўҳпјҢз”ЁеҚ•еҫӘзҺҜиөӣе…¬ејҸи§ЈйўҳгҖӮ
гҖҖгҖҖ第дәҢжӯҘпјҢз”ұжҜҸдёӘе°Ҹз»„4ж”ҜзҗғйҳҹиҝӣиЎҢеҚ•еҫӘзҺҜжҜ”иөӣпјҢеҸҜеҫ—жҜҸдёӘе°Ҹз»„еҶ…йғЁзҡ„жҜ”иөӣеңәж¬Ўж•°дёә(еңә)гҖӮ
гҖҖгҖҖ第дёүжӯҘпјҢ32ж”ҜзҗғйҳҹеҲҶжҲҗ8дёӘе°Ҹз»„пјҢжҜҸдёӘе°Ҹз»„йңҖиҰҒиҝӣиЎҢ6еңәжҜ”иөӣпјҢйӮЈд№Ҳж•ҙдёӘе°Ҹз»„иөӣйҳ¶ж®өжҜ”иөӣеңәж¬Ўж•°е…ұжңү8×6=48(еңә)гҖӮ
гҖҖгҖҖеӣ жӯӨпјҢйҖүжӢ©CйҖүйЎ№гҖӮ
гҖҖгҖҖгҖҗжӢ“еұ•гҖ‘
гҖҖгҖҖгҖҗж ҮзӯҫгҖ‘
гҖҖгҖҖгҖҗзҹҘиҜҶзӮ№гҖ‘жҜ”иөӣй—®йўҳ
гҖҖгҖҖгҖҗйҡҫеәҰгҖ‘дёӯзӯү
гҖҖгҖҖ2.жҡ‘еҒҮйҮҢд№җд№җжҠҘеҗҚеҸӮеҠ дәҶжёёжіігҖҒз»ҳз”»е’Ңи·ҶжӢійҒ“зӯүдёүдёӘе…ҙи¶ЈзҸӯпјҢе…¶дёӯжёёжіізҸӯжҜҸйҡ”2еӨ©дёҠдёҖж¬ЎиҜҫпјҢз»ҳз”»зҸӯжҜҸйҡ”3еӨ©дёҠдёҖж¬ЎиҜҫпјҢи·ҶжӢійҒ“жҜҸйҡ”6еӨ©дёҠдёҖж¬ЎиҜҫгҖӮе·ІзҹҘ7жңҲ1ж—Ҙд№җд№җеңЁиҝҷдёүдёӘе…ҙи¶ЈзҸӯйғҪдёҠдәҶиҜҫпјҢеҲҷд»–еңЁ7гҖҒ8дёӨдёӘжңҲдёӯдёҚз”ЁдёҠиҝҷдёүдёӘе…ҙи¶ЈзҸӯзҡ„еӨ©ж•°жҳҜ( )еӨ©гҖӮ
гҖҖгҖҖA.25
гҖҖгҖҖB.26
гҖҖгҖҖC.28
гҖҖгҖҖD.27
гҖҖгҖҖгҖҗзӯ”жЎҲгҖ‘D
гҖҖгҖҖгҖҗи§ЈжһҗгҖ‘
гҖҖгҖҖи§Јжі•дёҖпјҡ
гҖҖгҖҖ第дёҖжӯҘпјҢжң¬йўҳиҖғжҹҘжҳҹжңҹж—Ҙжңҹй—®йўҳпјҢз”Ёжһҡдёҫжі•и§ЈйўҳгҖӮ
гҖҖгҖҖ第дёҖжӯҘпјҢ7жңҲ1ж—ҘдёүдёӘе…ҙи¶ЈзҸӯйғҪдёҠдәҶиҜҫпјҢеҲҷ7—8жңҲдёӯпјҢдёҠиҜҫжғ…еҶөеҰӮдёӢиЎЁпјҡ
гҖҖгҖҖ(дёҠжёёжііиҜҫз”Ё√пјҢдёҠз»ҳз”»иҜҫз”Ёв—ӢпјҢдёҠи·ҶжӢійҒ“иҜҫз”Ёв–іпјҢж— иҜҫз”Ё×)
| 7—8жңҲ | ||||||
| 1 | 2 | 4 | 5 | 6 | 7 | |
| √в—Ӣв–і | × | × | √ | в—Ӣ | × | √ |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| в–і | в—Ӣ | √ | × | × | √в—Ӣ | × |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| в–і | √ | в—Ӣ | × | √ | × | в—Ӣ |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| √в–і | × | × | √в—Ӣ | × | × | √ |
| 29 | 30 | 31 | 1 | 2 | 3 | 4 |
| в—Ӣв–і | × | √ | × | в—Ӣ | √ | × |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| в–і | √в—Ӣ | × | × | √ | в—Ӣ | × |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| √в–і | × | в—Ӣ | √ | × | × | √в—Ӣ |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| в–і | × | √ | в—Ӣ | × | √ | × |
| 26 | 27 | 28 | 29 | 30 | 31 | |
| в—Ӣв–і | √ | × | × | √в—Ӣ | × | |
гҖҖгҖҖе…ұжңү27еӨ©дёҚз”ЁдёҠиҝҷдёүдёӘе…ҙи¶ЈзҸӯгҖӮ
гҖҖгҖҖеӣ жӯӨпјҢйҖүжӢ©DйҖүйЎ№гҖӮ
гҖҖгҖҖи§Јжі•дәҢпјҡ
гҖҖгҖҖ第дёҖжӯҘпјҢжң¬йўҳиҖғжҹҘжҳҹжңҹж—Ҙжңҹй—®йўҳпјҢз”Ёе®№ж–ҘеҺҹзҗҶзӣёе…ізҹҘиҜҶи§ЈйўҳгҖӮ
гҖҖгҖҖ第дәҢжӯҘпјҢ7жңҲе’Ң8жңҲйғҪжҳҜеӨ§жңҲпјҢеҗ„жңү31еӨ©пјҢе…ұ62еӨ©пјҢ7жңҲ1ж—ҘдёүдёӘиҜҫйғҪдёҠпјҢеҸӘи®Ёи®әеү©дёӢзҡ„61еӨ©пјҢжёёжіізҸӯдёҠиҜҫ61÷3=20……1пјҢеҚідёҠиҜҫ20еӨ©;з»ҳз”»зҸӯдёҠиҜҫ61÷4=15……1пјҢеҚідёҠиҜҫ15еӨ©;и·ҶжӢійҒ“зҸӯдёҠиҜҫ61÷7=8……5пјҢеҚідёҠиҜҫ8еӨ©гҖӮеҗҢж—¶дёҠжёёжііе’Ңз»ҳз”»зҸӯзҡ„жңү61÷12(3е’Ң4зҡ„жңҖе°Ҹе…¬еҖҚж•°)=5……1пјҢеҚі5еӨ©;еҗҢж—¶дёҠжёёжііе’Ңи·ҶжӢійҒ“зҸӯзҡ„жңү61÷21=2……19;еҗҢж—¶дёҠз»ҳз”»е’Ңи·ҶжӢійҒ“зҸӯзҡ„жңү61÷28=2……5пјҢеҚі2еӨ©пјҢдёүдёӘиҜҫйғҪдёҠзҡ„жІЎжңүпјҢеӣ жӯӨе…ұдёҠиҜҫ20+15+8-5-2-2=34(еӨ©)пјҢйӮЈд№Ҳжңү61-34=27(еӨ©)дёүдёӘиҜҫйғҪдёҚз”ЁдёҠгҖӮ
гҖҖгҖҖеӣ жӯӨпјҢйҖүжӢ©DйҖүйЎ№гҖӮ
гҖҖгҖҖгҖҗжӢ“еұ•гҖ‘
гҖҖгҖҖгҖҗж ҮзӯҫгҖ‘
гҖҖгҖҖгҖҗзҹҘиҜҶзӮ№гҖ‘жҳҹжңҹж—Ҙжңҹй—®йўҳ
гҖҖгҖҖгҖҗйҡҫеәҰгҖ‘дёӯзӯү
гҖҖгҖҖ3.1896пјҢ1948пјҢ1988пјҢ2000пјҢ2012пјҢ2020пјҢдёӢеҲ—е№ҙеәҰдёӯдёҺдёҠиҝ°е№ҙеәҰе…·жңүзӣёеҗҢзҡ„规еҫӢзҡ„е№ҙеәҰжҳҜ( )е№ҙгҖӮ
гҖҖгҖҖA.1600
гҖҖгҖҖB.1900
гҖҖгҖҖC.2010
гҖҖгҖҖD.2018
гҖҖгҖҖгҖҗзӯ”жЎҲгҖ‘A
гҖҖгҖҖгҖҗи§ЈжһҗгҖ‘
гҖҖгҖҖ第дёҖжӯҘпјҢжң¬йўҳиҖғжҹҘжҳҹжңҹж—Ҙжңҹй—®йўҳгҖӮ
гҖҖгҖҖ第дәҢжӯҘпјҢж №жҚ®й—°е№ҙеҲӨе®ҡжі•еҲҷпјҡйқһж•ҙзҷҫе№ҙе№ҙд»ҪиғҪиў«4ж•ҙйҷӨжҲ–ж•ҙзҷҫе№ҙд»ҪиғҪиў«400ж•ҙйҷӨзҡ„дёәй—°е№ҙгҖӮйўҳе№Ідёӯз»ҷеҮәзҡ„1896пјҢ1948пјҢ1988пјҢ2000пјҢ2012пјҢ2020йғҪжҳҜй—°е№ҙпјҢи§ӮеҜҹйҖүйЎ№еҸ‘зҺ°пјҢеҸӘжңү1600е№ҙжҳҜй—°е№ҙгҖӮ
гҖҖгҖҖеӣ жӯӨпјҢйҖүжӢ©AйҖүйЎ№гҖӮ
гҖҖгҖҖгҖҗжӢ“еұ•гҖ‘
гҖҖгҖҖгҖҗж ҮзӯҫгҖ‘
гҖҖгҖҖгҖҗзҹҘиҜҶзӮ№гҖ‘жҳҹжңҹж—Ҙжңҹй—®йўҳ
гҖҖгҖҖгҖҗйҡҫеәҰгҖ‘дёӯзӯү
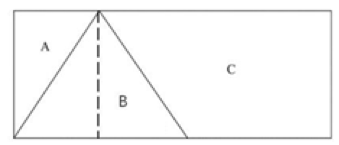
гҖҖгҖҖ4.е°ҶдёҖеқ—й•ҝ10еҺҳзұігҖҒе®Ҫ4еҺҳзұізҡ„й•ҝж–№еҪўе№іжқҝеҲҮеүІжҲҗAгҖҒBгҖҒCе…ұ3еқ—пјҢе…¶дёӯCеқ—зҡ„йқўз§Ҝдёә22е№іж–№еҺҳзұіпјҢBдёәзӯүи…°дёүи§’еҪўпјҢйӮЈд№ҲAеқ—зҡ„йқўз§ҜжҳҜ( )гҖӮ
 гҖҖгҖҖA.6е№іж–№еҺҳзұі
гҖҖгҖҖA.6е№іж–№еҺҳзұігҖҖгҖҖB.12е№іж–№еҺҳзұі
гҖҖгҖҖC.8е№іж–№еҺҳзұі
гҖҖгҖҖD.4е№іж–№еҺҳзұі
гҖҖгҖҖгҖҗзӯ”жЎҲгҖ‘A
гҖҖгҖҖгҖҗи§ЈжһҗгҖ‘
гҖҖгҖҖ第дёҖжӯҘпјҢжң¬йўҳиҖғжҹҘеҮ дҪ•й—®йўҳпјҢеұһдәҺе№ійқўеҮ дҪ•зҡ„йқўз§Ҝи®Ўз®—й—®йўҳгҖӮ
гҖҖгҖҖ第дәҢжӯҘпјҢй•ҝж–№еҪўзҡ„й•ҝдёә10еҺҳзұіпјҢе®Ҫдёә4еҺҳзұіпјҢйӮЈд№ҲиҜҘзҹ©еҪўзҡ„йқўз§Ҝдёә10×4=40(е№іж–№еҺҳзұі)пјҢCзҡ„йқўз§Ҝдёә22е№іж–№еҺҳзұіпјҢйӮЈд№ҲA+Bзҡ„йқўз§Ҝдёә40-22=18(е№іж–№еҺҳзұі)гҖӮеҒҡдёүи§’еҪўBзҡ„еһӮзәҝпјҢеҰӮеӣҫжүҖзӨәпјҢBдёәзӯүи…°дёүи§’еҪўпјҢеҲҷдёүзәҝеҗҲдёҖпјҢйӮЈд№ҲеҸҜеҫ—дёүи§’еҪўAзҡ„йқўз§Ҝдёәдёүи§’еҪўBзҡ„йқўз§Ҝзҡ„дёҖеҚҠпјҢеҲҷв–іBзҡ„йқўз§Ҝ=2×в–іAзҡ„йқўз§ҜгҖӮйӮЈд№Ҳв–іAзҡ„йқўз§Ҝдёә18/3=6(е№іж–№еҺҳзұі)гҖӮ

гҖҖгҖҖеӣ жӯӨпјҢйҖүжӢ©AйҖүйЎ№гҖӮ
гҖҖгҖҖгҖҗжӢ“еұ•гҖ‘
гҖҖгҖҖгҖҗж ҮзӯҫгҖ‘
гҖҖгҖҖгҖҗзҹҘиҜҶзӮ№гҖ‘е№ійқўеҮ дҪ•зұ»
гҖҖгҖҖгҖҗйҡҫеәҰгҖ‘дёӯзӯү
гҖҖгҖҖ5.е·ҘеҺӮз”ҹдә§дёҖжү№дә§е“ҒпјҢ18еҗҚе·ҘдәәйңҖ3.5е°Ҹж—¶жүҚиғҪе®ҢжҲҗгҖӮзҺ°йңҖжҸҗеүҚ0.5е°Ҹж—¶е®ҢжҲҗпјҢеҒҮи®ҫе·Ҙдәәе·ҘдҪңж•ҲзҺҮзӣёеҗҢпјҢеҲҷйңҖеўһеҠ е·Ҙдәәзҡ„дәәж•°жҳҜ( )дәәгҖӮ
гҖҖгҖҖA.1
гҖҖгҖҖB.2
гҖҖгҖҖC.3
гҖҖгҖҖD.4
гҖҖгҖҖгҖҗзӯ”жЎҲгҖ‘C
гҖҖгҖҖгҖҗи§ЈжһҗгҖ‘
гҖҖгҖҖ第дёҖжӯҘпјҢжң¬йўҳиҖғжҹҘе·ҘзЁӢй—®йўҳпјҢз”ЁиөӢеҖјжі•и§ЈйўҳгҖӮ
гҖҖгҖҖ第дәҢжӯҘпјҢиөӢеҖјжҜҸеҗҚе·Ҙдәәзҡ„ж•ҲзҺҮдёә1пјҢйӮЈд№Ҳ18еҗҚе·Ҙдәәзҡ„ж•ҲзҺҮдёә18пјҢйңҖиҰҒ3.5е°Ҹж—¶жүҚиғҪе®ҢжҲҗпјҢиҜҙжҳҺиҝҷжү№дә§е“Ғзҡ„жҖ»йҮҸдёә18×3.5=63пјҢиҰҒжғіжҸҗеүҚ0.5е°Ҹж—¶е®ҢжҲҗпјҢеҲҷз”Ёж—¶3.5-0.5=3(е°Ҹж—¶)пјҢйӮЈд№Ҳж•ҲзҺҮйңҖиҰҒиҫҫеҲ°63/3=21пјҢеҚійңҖиҰҒ21еҗҚе·ҘдәәпјҢйңҖиҰҒеўһеҠ 21-18=3(дәә)гҖӮ
гҖҖгҖҖеӣ жӯӨпјҢйҖүжӢ©CйҖүйЎ№гҖӮ
гҖҖгҖҖгҖҗжӢ“еұ•гҖ‘
гҖҖгҖҖгҖҗж ҮзӯҫгҖ‘
гҖҖгҖҖгҖҗзҹҘиҜҶзӮ№гҖ‘ж•ҲзҺҮзұ»
гҖҖгҖҖгҖҗйҡҫеәҰгҖ‘дёӯзӯү










