гҖҖгҖҖжҜ”йҮҚжҳҜйғЁеҲҶйҷӨд»Ҙж•ҙдҪ“еҗҺпјҢд»ҘзҷҫеҲҶж•°еҪўејҸиЎЁзӨәзҡ„з»“жһңпјҢеёёи§ҒиҖғжі•дёәжҜ”йҮҚзҡ„и®Ўз®—дёҺжҜ”иҫғгҖӮеҜ№дәҺжҜ”иҫғзұ»йўҳзӣ®иҖҢиЁҖпјҢ常规жҖқи·ҜеҫҖеҫҖжҳҜз®—еҮәжҜҸдёҖйЎ№зҡ„жҜ”йҮҚд№ӢеҗҺпјҢжҜ”иҫғе…¶еӨ§е°ҸпјҢдҪҶжҳҜиҝҷж ·еҒҡжңүеҸҜиғҪи®Ўз®—йҮҸжҜ”иҫғеӨ§гҖӮеҰӮжһңиғҪеӨҹеҮҸе°‘и®Ўз®—йҮҸпјҢз”ҡиҮідёҚйңҖи®Ўз®—пјҢзӣҙжҺҘжҜ”иҫғеӨ§е°ҸпјҢеҲҷдәӢеҚҠеҠҹеҖҚпјҢиҝҷйңҖиҰҒе…·еӨҮд»ҘдёӢдёӨз§ҚжҖқз»ҙпјҡ
гҖҖгҖҖжҖқз»ҙдёҖпјҡйғЁеҲҶжҖқз»ҙ
гҖҖгҖҖгҖҗдҫӢ1гҖ‘
гҖҖгҖҖ(2019иҒ”иҖғ)
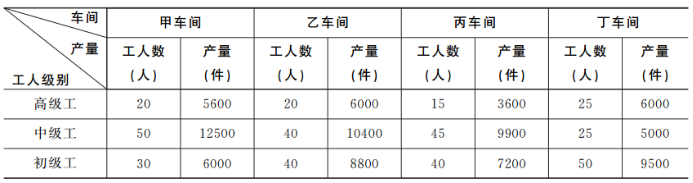
гҖҖгҖҖжҹҗжңәжў°еҠ е·ҘдјҒдёҡдёӢи®ҫеӣӣдёӘз”ҹдә§иҪҰй—ҙз”ҹдә§еҠ е·ҘеҗҢз§Қзұ»еһӢе’ҢеһӢеҸ·зҡ„дә§е“ҒпјҢ并д»ҘдәәеқҮдә§йҮҸиҜ„д»·еҠіеҠЁз”ҹдә§зҺҮгҖӮ
гҖҖгҖҖжң¬иҪҰй—ҙдёӯдёӯзә§е·ҘеҚ жҜ”жңҖеӨ§зҡ„жҳҜпјҡ
гҖҖгҖҖA.з”І
гҖҖгҖҖB.д№ҷ
гҖҖгҖҖC.дёҷ
гҖҖгҖҖD.дёҒ
гҖҖгҖҖгҖҗзӯ”жЎҲгҖ‘A
гҖҖгҖҖгҖҗи§ЈжһҗгҖ‘ж №жҚ®й—®жі•“еҚ жҜ”жңҖеӨ§”еҲӨе®ҡдёәжҜ”йҮҚжҜ”иҫғпјҢ常规жҖқи·ҜпјҢжұӮеҮәжҜҸдёӘйҖүйЎ№зҡ„жҜ”йҮҚгҖӮдҪҶжҳҜиҝӣдёҖжӯҘеҸ‘зҺ°пјҢжүҖжңүиҪҰй—ҙеҗ„иҮӘзҡ„жҖ»дәәж•°еқҮдёә100дәәпјҢеҚі“ж•ҙдҪ“зӣёеҗҢ”пјҢжӯӨж—¶пјҢйғЁеҲҶи¶ҠеӨ§пјҢеҲҷжүҖеҚ жҜ”йҮҚи¶ҠеӨ§гҖӮж•…зӣҙжҺҘжҜ”иҫғеӣӣдёӘйҖүйЎ№зҡ„йғЁеҲҶеӨ§е°ҸпјҢд№ҹе°ұжҳҜдёӯзә§е·Ҙзҡ„ж•°йҮҸеӨ§е°ҸпјҢеӣӣдёӘйҖүйЎ№еҲҶеҲ«дёә50гҖҒ40гҖҒ45гҖҒ25пјҢжҳҫ然AйЎ№дёӯзҡ„“50”жҳҜжңҖеӨ§зҡ„пјҢж•…йҖүжӢ©AйЎ№гҖӮ
гҖҖгҖҖгҖҗдҫӢ2гҖ‘
гҖҖгҖҖ(2019з”ҳиӮғ)еҮәеҸЈж–№йқўпјҢ2018е№ҙ第дёҖеӯЈеәҰжҲ‘еӣҪж°ҙдә§е“ҒеҮәеҸЈйҮҸ98.04дёҮеҗЁпјҢеҗҢжҜ”еҮҸе°‘2.7%пјҢеҮәеҸЈйўқ48.41дәҝзҫҺе…ғпјҢеўһеҠ 5.90%гҖӮдёҖиҲ¬иҙёжҳ“еҮәеҸЈйҮҸ71.18дёҮеҗЁпјҢеҗҢжҜ”еҮҸе°‘4.06%;еҮәеҸЈйўқ36.71дәҝзҫҺе…ғпјҢеҗҢжҜ”еўһеҠ 6.22%гҖӮ

гҖҖгҖҖ2018е№ҙ第дёҖеӯЈеәҰпјҢжҲ‘еӣҪж°ҙдә§е“ҒдёҖиҲ¬иҙёжҳ“дё»иҰҒеҮәеҸЈе“Ғз§ҚдёӯпјҢеҮәеҸЈйўқеҚ жҲ‘еӣҪж°ҙдә§е“ҒдёҖиҲ¬иҙёжҳ“еҮәеҸЈйўқзҡ„жҜ”йҮҚпјҢи¶…иҝҮ5%зҡ„жңүеҮ дёӘ?
гҖҖгҖҖA.5
гҖҖгҖҖB.6
гҖҖгҖҖC.7
гҖҖгҖҖD.8
гҖҖгҖҖгҖҗзӯ”жЎҲгҖ‘B
гҖҖгҖҖгҖҗи§ЈжһҗгҖ‘常规жҖқи·ҜжұӮеҮәжҜҸдёҖдёӘе“Ғз§ҚжүҖеҚ зҡ„жҜ”йҮҚпјҢдёҺ5%жҜ”иҫғеӨ§е°ҸпјҢеҚҒеҲҶеӨҚжқӮгҖӮдҪҶжҳҜз”ұдәҺйғҪжҳҜ“еҚ жҲ‘еӣҪж°ҙдә§е“ҒдёҖиҲ¬иҙёжҳ“еҮәеҸЈйўқзҡ„жҜ”йҮҚ”пјҢж•…ж•ҙдҪ“жҳҜдёҖж ·зҡ„пјҢе®Ңе…ЁеҸҜд»ҘжұӮеҮә“и¶…иҝҮ5%”зҡ„ж—¶еҖҷпјҢйғЁеҲҶзҡ„ж ҮеҮҶжҳҜеӨҡе°‘гҖӮз®ҖеҚ•и®Ўз®—пјҢ“еҮәеҸЈйўқ36.71дәҝзҫҺе…ғ”зҡ„5%дёәпјҡ36.71×5%=1.8355дәҝзҫҺе…ғпјҢиЎЁж јеҪ“дёӯеҮәеҸЈйўқеӨ§дәҺ1.8355зҡ„жңүеӨҙи¶ізұ»гҖҒеҜ№иҷҫгҖҒиҙқзұ»гҖҒзҪ—йқһйұјгҖҒйі—йұјгҖҒиҹ№зұ»пјҢеҗҲи®Ў6зұ»пјҢж•…йҖүжӢ©BйЎ№гҖӮ
гҖҖгҖҖгҖҗжҖ»з»“гҖ‘ж №жҚ®д»ҘдёҠдёӨйўҳпјҢе…¶е…ұеҗҢзӮ№дёә“ж•ҙдҪ“зӣёеҗҢ”пјҢеҲҷжӯӨж—¶жҜ”иҫғжҜ”йҮҚзҡ„еӨ§е°ҸпјҢе®һиҙЁжҳҜжҜ”иҫғйғЁеҲҶзҡ„еӨ§е°ҸпјҢиҝҷж ·жүҚиғҪе°‘иө°ејҜи·ҜгҖӮ
гҖҖгҖҖжҖқз»ҙдәҢпјҡиҪ¬еҢ–жҖқз»ҙ
гҖҖгҖҖгҖҗдҫӢ3гҖ‘
гҖҖгҖҖ(2017иҒ”иҖғ)2015е№ҙе…ЁеӣҪе…ұе»әз«ӢзӨҫдјҡжҚҗеҠ©е·ҘдҪңз«ҷгҖҒзӮ№е’Ңж…Ҳе–„и¶…еёӮ3.0дёҮдёӘпјҢжҜ”дёҠдёҖе№ҙеҮҸе°‘0.2дёҮдёӘпјҢе…¶дёӯпјҡж…Ҳе–„и¶…еёӮ9654дёӘпјҢеҗҢжҜ”дёӢйҷҚ5.1%гҖӮе…Ёе№ҙе…ұжҺҘ收зӨҫдјҡжҚҗиө ж¬ҫ654.5дәҝе…ғпјҢе…¶дёӯпјҡж°‘ж”ҝйғЁй—ЁжҺҘ收зӨҫдјҡеҗ„з•ҢжҚҗж¬ҫ44.2дәҝе…ғпјҢеҗ„зұ»зӨҫдјҡз»„з»ҮжҺҘ收жҚҗж¬ҫ610.3дәҝе…ғгҖӮ
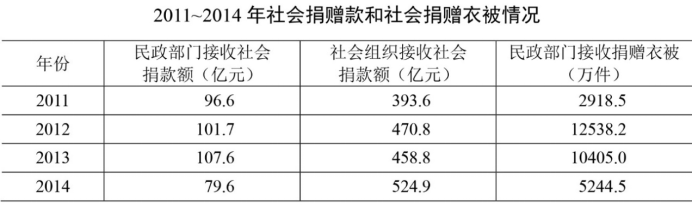
гҖҖгҖҖ2012-2015е№ҙзӨҫдјҡз»„з»ҮжҺҘ收зӨҫдјҡжҚҗиө ж¬ҫеҚ жҖ»жҚҗиө ж¬ҫзҡ„жҜ”йҮҚжңҖй«ҳзҡ„жҳҜпјҡ
гҖҖгҖҖA.2012е№ҙ
гҖҖгҖҖB.2013е№ҙ
гҖҖгҖҖC.2014е№ҙ
гҖҖгҖҖD.2015е№ҙ
гҖҖгҖҖгҖҗзӯ”жЎҲгҖ‘D
гҖҖгҖҖгҖҗи§ЈжһҗгҖ‘常规жҖқи·ҜжұӮеҮәжҖ»жҚҗиө йўқпјҢеҶҚз®—еҮәжҜ”йҮҚпјҢйңҖиҰҒдёӨжӯҘи®Ўз®—пјҢи®Ўз®—жӯҘйӘӨиҫғеӨҡгҖӮз”ұдәҺжҖ»жҚҗж¬ҫйўқеҸӘеҢ…еҗ«зӨҫдјҡз»„з»ҮжҚҗиө е’Ңж°‘ж”ҝйғЁй—ЁжҺҘ收зҡ„жҚҗиө дёӨдёӘйғЁеҲҶпјҢе°ұеғҸдёҖдёӘзҸӯд»…д»…еҢ…жӢ¬з”·з”ҹе’ҢеҘіз”ҹдёҖж ·пјҢжӯӨж—¶йўҳе№ІзӣёеҪ“дәҺй—®з”·з”ҹеҚ жҜ”жңҖеӨ§зҡ„жҳҜе“ӘдёӘзҸӯпјҢе®Ңе…Ёзӯүд»·дәҺз”·з”ҹзӣёжҜ”еҘіз”ҹзҡ„еҖҚж•°жңҖеӨ§зҡ„е“ӘдёӘзҸӯгҖӮ
гҖҖгҖҖж•…жң¬йўҳиҪ¬еҢ–дёә“зӨҫдјҡз»„з»ҮжҺҘ收жҚҗиө ж¬ҫзӣёжҜ”ж°‘ж”ҝйғЁй—ЁжҺҘ收зҡ„жҚҗиө ж¬ҫ”зҡ„еҖҚж•°жңҖеӨ§зҡ„жҳҜе“ӘдёҖж ·пјҢз®ҖеҚ•з®—дёҖдёӢпјҢеӣӣдёӘйҖүйЎ№еҲҶеҲ«дёәпјҡ470.8÷101.7гҖҒ458.8÷107.6гҖҒ524.9÷79.6гҖҒ610.3÷44.2пјҢеүҚдёүйЎ№зҡ„з»“жһңйғҪдёҚи¶і10пјҢ第еӣӣйЎ№зҡ„з»“жһңи¶…иҝҮ10пјҢ故第еӣӣйЎ№жңҖеӨ§пјҢж•…йҖүжӢ©DйҖүйЎ№гҖӮ
гҖҖгҖҖгҖҗжҖ»з»“гҖ‘еҪ“и®Ўз®—жӯҘйӘӨиҫғеӨҡж—¶пјҢйҖҡиҝҮиҪ¬еҢ–пјҢиҪ¬еҢ–дёәжӯҘйӘӨиҫғе°‘зҡ„жғ…еҶөпјҢеҶҚи®Ўз®—гҖӮзЈЁеҲҖдёҚиҜҜз Қжҹҙе·ҘпјҢе…Ҳз®ҖеҢ–жӯҘйӘӨпјҢеҶҚиҖғиҷ‘еёҰе…Ҙж•°еӯ—и®Ўз®—пјҢиҝҷж ·жүҚиғҪе°‘иө°ејҜи·ҜгҖӮ











